Yksi askel! Antenni kaikenlaisia laskentakaavan yhteenveto
Arvioitu 8 minuuttia lukemisen loppuun
Antennien eri tärkeiden parametrien esittelyn jälkeen siirrymme syvemmälle alueelle, joka on parametreihin liittyvät laskentakaavat. Jokainen kaava tuo paljon mukavuutta ennen asennusta ja sen jälkeen. Nämä kaavat on tiivistetty tässä numerossa, ei vain voi ratkaista erilaisia kysymyksiä käytön aikana, vaan myös antaa ideoita myöhempää antenniasettelua varten .
Antennivahvistus on parametri, jolla mitataan antennin säteilyn suuntakartan suuntausastetta. Vahva antenni antaa etusijalle tietyn säteilysuunnan. Antennivahvistus on passiivinen ilmiö, antenni ei lisää tehoa, vaan se yksinkertaisesti jaetaan uudelleen, jotta saadaan enemmän säteilytehoa tiettyyn suuntaan kuin muut isotrooppiset antennit lähettävät.
↓ Seuraavassa on joitain likimääräisiä yhtälöitä antennin vahvistukselle.
Yleinen antenni
G(dBi) = 10 Lg { 32000 / (2θ3dB,E × 2θ3dB,H)}
Kaavassa 2θ3dB,E ja 2θ3dB,H ovat antenniläppien leveys kahdessa päätasossa, vastaavasti; 32000 on tilastollinen empiirinen data.
Parabolinen antenni
G (dBi) = 10Lg{4,5×(D/λ0)2}
Kaavassa D on paraboloidin halkaisija; λ0 on keskimmäinen toiminta-aallonpituus; 4.5 on tilastollinen empiirinen data.
Pystysuuntainen monisuuntainen antenni
G(dBi) = 10 Lg { 2 L / λ0 }
Kaavassa L on antennin pituus; λ0 on keskimmäinen toiminta-aallonpituus.
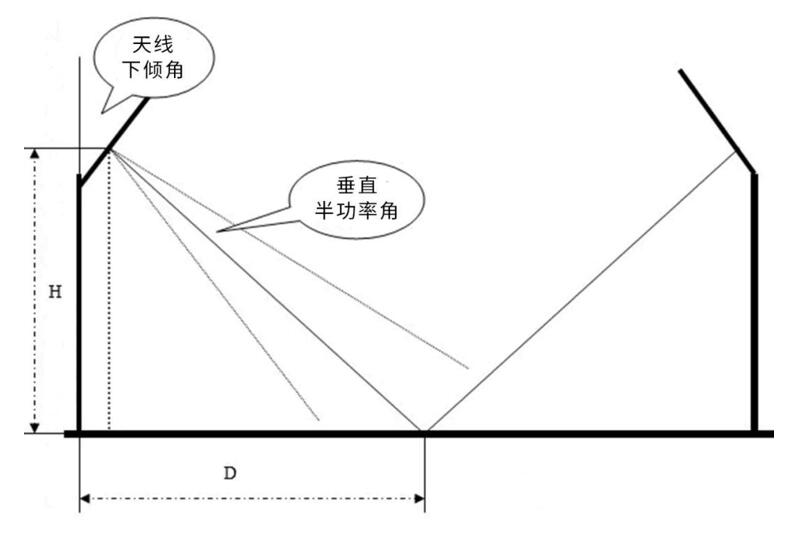
Antennisäädössä tärkeintä on sen alaskallistuskulman hienosäätö (mikä voi ratkaista heikon peiton päällekkäisen peiton ongelmat jne.). Seuraavassa on johdatus sen alkuperäisimpään antennin kallistuskulman laskentamenetelmään.
Antennilaskentakaava vilkkaasti liikennöidylle alueelle (kaupunkialue).
Antennin kallistuskulma = arctag(H/D) + pystysuuntainen puolitehokulma / 2
Matala palvelualue (maaseutu, esikaupunkialueet jne.) antennikaava .
Antennin kallistuskulma = kaarimerkki (K/D)
Parametrin kuvaus.
(1) antennin kallistuskulma: antennin ja pystysuunnan välinen kulma.
(2) H: antennin korkeus. Se voidaan mitata suoraan.
(3) D: solun peittosäde. Yleensä D-arvo määritetään tietestillä peiton varmistamiseksi varsinaisessa suunnittelussa, yleensä D:n tulisi olla suurempi, jotta varmistetaan peittopäällekkäisyys naapurisolujen välillä.
(4) Pystysuuntainen puolitehokulma: antennin pystysuuntainen puolitehokulma, yleensä 10 astetta.
Suuntakaavio, etu- ja takaläpän maksimiarvon suhdetta kutsutaan etu- ja takasuhteeksi, joka kirjataan F / B . Ennen ja jälkeen kuin suurempi, antenni säteilyn (tai vastaanoton) jälkeen on pienempi. Ennen ja jälkeen F / B -suhde on erittäin helppo laskea:
F / B = 10 Lg {(tehotiheys eteenpäin) / (taaksepäin tehotiheys)}
Parametrin kuvaus: antennin etu-takasuhde F / B vaatimukset, sen tyypillinen arvo on (18 ~ 30) dB, erityisolosuhteet vaativat jopa (35 ~ 40) dB.
Signaalijännitteen ja signaalivirran suhdetta antennin sisäänmenossa kutsutaan antennin tuloimpedanssiksi. Tuloimpedanssilla on resistanssikomponentti Rin ja reaktanssikomponentti Xin, eli.
Zin = Rin + j Xin
Reaktanssikomponentin olemassaolo pienentää antennin syöttölinjasta signaalin tehonpoistoon, joten reaktanssikomponentti tulee tehdä mahdollisimman pitkälle nollaksi, eli antennin tuloimpedanssin tulisi olla mahdollisimman pitkälle puhdasta vastusta varten.
Itse asiassa, vaikka antenni olisi hyvin suunniteltu ja otettu käyttöön, tuloimpedanssi sisältää aina pienen reaktanssikomponentin arvon. Tuloimpedanssi ja antennin rakenne, koko ja aallonpituus, puoliaaltosymmetrinen oskillaattori on tärkein perusantenni.
Sen tuloimpedanssi on Zin = 73,1 + j42,5 (ohm).
Kun pituutta lyhennetään (3-5)%, reaktanssikomponentti voidaan eliminoida siten, että antennin tuloimpedanssi on puhdasta resistanssia, jolloin tuloimpedanssi on Zin = 73,1 ohmia (nimellinen 75 ohmia). Tarkkaan ottaen puhtaasti resistiivinen antennin tuloimpedanssi on vain pistetaajuudelle. Muuten, puoliaaltotaitetun oskillaattorin tuloimpedanssi on neljä kertaa puoliaaltosymmetrinen oskillaattori, eli Zin = 280 ohmia (nimellinen 300 ohmia).
Jännitteen ja virran suhde äärettömän pitkän siirtojohdon eri kohdissa määritellään siirtojohdon ominaisimpedanssiksi ja sitä merkitään Z:lla. Koaksiaalikaapelin ominaisimpedanssin laskentakaava on:
Z = [60/√εr] × Log ( D/d ) [ohm
Kaavassa D on koaksiaalikaapelin ulkojohtimen kupariverkon sisähalkaisija; d on koaksiaalikaapelin sydämen ulkohalkaisija; εr on johtimien välisen eristysaineen suhteellinen dielektrisyysvakio. Huomautus: Yleensä Z. = 50 ohmia, on myös Z. = 75 ohmia.
Yllä olevasta kaavasta on helppo nähdä, että syöttöjohdon ominaisimpedanssi liittyy vain johtimen halkaisijaan D ja d sekä johtimien väliseen dielektrisyysvakioon εr, mutta ei syöttöjohdon pituuteen, toimintataajuuteen ja kytkettyyn kuormitusimpedanssiin. syöttölinjan terminaaliin.
Signaalin siirto syöttölaitteessa johtimen resistiivisen häviön lisäksi eristemateriaalissa on dielektristä häviötä. Nämä kaksi häviötä kasvavat syöttölaitteen pituuden ja käyttötaajuuden kasvaessa. Siksi järkevän asettelun tulee olla mahdollisimman lyhyt syöttölaitteen pituuden lyhentämiseksi.
Häviön suuruus pituusyksikköä kohti ilmaistaan vaimennuskertoimella β, jonka yksikkö on dB / m (desibeli / metri), kaapelin teknisten eritelmien yksikkö enimmäkseen käytetyn dB / 100m (desibeli / sata metriä).
Olkoon syöttöteho syöttölaitteeseen P1, lähtöteho L (m) syöttölaitteen pituudesta on P2, siirtohäviö TL voidaan ilmaista seuraavasti.
TL = 10 × Lg ( P1 / P2 ) ( dB )
Vaimennuskerroin on: β = TL / L ( dB / m )
Epäsopivuustapauksessa syöttölinjalla on sekä saapuvia että heijastuneita aaltoja. Paikassa, jossa tulevat ja heijastuneet aallot ovat samassa vaiheessa, jänniteamplitudit summautuvat maksimijänniteamplitudiin Vmax muodostaen aaltoraidan; kun taas paikassa, jossa tulevat ja heijastuneet aallot ovat vastakkaisessa vaiheessa, jänniteamplitudit vähentävät minimijänniteamplitudia Vmin muodostaen aaltosolmun. Muiden pisteiden amplitudiarvot ovat aaltovatsan ja aaltosolmun välissä. Tätä synteettistä aaltoa kutsutaan seisovaksi aalloksi.
A, heijastuneen aaltojännitteen ja tulevan aallon jännitteen amplitudin suhdetta kutsutaan heijastuskertoimeksi, joka merkitään R:llä.
R = heijastuneen aallon amplitudi / tulevan aallon amplitudi = (ZL - Z0) / (ZL + Z0 )
Toiseksi aaltovatsajännitteen suhdetta aaltoosan jänniteamplitudiin kutsutaan seisova-aaltokertoimeksi, joka tunnetaan myös jännitteen seisova-aaltosuhteena, joka merkitään nimellä VSWR : VSWR = aaltovatsajänniteamplitudi.
VSWR = Vmax / Vmin = (1 + R) / (1-R)
Mitä lähempänä terminaalin kuormitusimpedanssi ZL ja ominaisimpedanssi Z0, sitä pienempi heijastuskerroin R, sitä lähempänä arvoa VSWR on 1 ja sitä parempi yhteensopivuus.


















 5G verkkoantenni
5G verkkoantenni